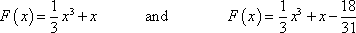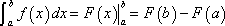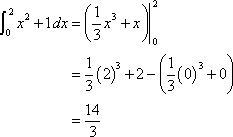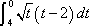Definite Integrals

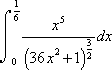
What is a Definite Integral?

A Definite Integral is an integral where there are upper and lower bounds. In other words, there are upper and lower limits. Usually these limits can be either numbers or functions. On this site, we will only be looking at numbers for the bounds. The final answer you get is the area between both bounds on a graph. There is a proof for this (Riemann's Sum), but this site won't go over it. See other sites if you want to learn more. All you have to know is that a definite integral is like a regular integral, but with upper and lower limits (and a few extra steps). Now, let's look at the following example:

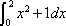
Now, the best way to approach this problem is to treat it like a regular integral problem. In this problem, we don't have to use Subsitution Rule. Therefore, take the integral of this. The answer would be this:

Now these next few steps are different. The answer you got from the integrand is not the final answer. This is because we now have upper and lower limits. Let's assume a=0 and b=2. Now, in order to find the area, you must plug in b (always b first) into your function (the function being the answer you got from the integrand) and subtract it by the function in which you plug in a. It will look something like this: integrandfinal

Using this formula, we get a final answer of this:
integrandfinal

Got the hang of it? Great! Now, try this example out!: example1