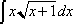Geometric
-
Integrals
Definite Integrals
Substitution
Integration by Parts
- References
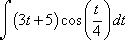
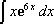
Now, let's split this. We will make x equal to "u" and e^6x equal to "dv" where "u" represents a function and "dv" represents the derivative of a function. Now, do the derivative and anti-derivative of the following variables:
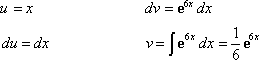
Once done, use this following formula. This formula includes a difference of a product and a integrand. Remembering this formula is crucial:
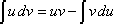
Apply the formula and you will get an answer like this:
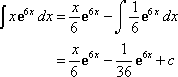
Do not forget to add a constant (represented by the letter C since we do not know the exact number). When differentiating without upper and lower limits, adding a constant is manditory.
Now that you've understood this, try out this example:
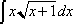
Integration by Parts
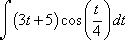
What is Integration by Parts?
Integration by Parts is a method used to solve an integral. It is usually applied when you have two different types of functions and a product of those functions. This method of integration involves you doing the derivatives and anti-derivatives of functions. Once done, you subtract a product and an integrand. This method of integration is very different from all of the others we have discussed so far. Now let's take a look at this example:
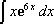
Now, let's split this. We will make x equal to "u" and e^6x equal to "dv" where "u" represents a function and "dv" represents the derivative of a function. Now, do the derivative and anti-derivative of the following variables:
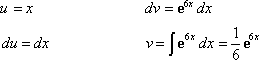
Once done, use this following formula. This formula includes a difference of a product and a integrand. Remembering this formula is crucial:
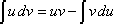
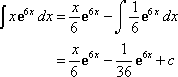
Now that you've understood this, try out this example: