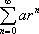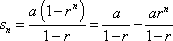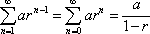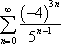Geometric
-
Integrals
Definite Integrals
Substitution
Integration by Parts
- References
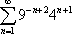
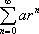
Now I'm sure you learned what a series is being convergent or divergent so I won't go over it. In order for this series to be convergent, the common ratio must be less than or equal to one (the common ratio must be taken as an absolute value). If the series is convergent, you find its sum by using this formula:
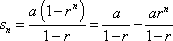
Why don't we make this formula a bit easier? Here, I'll prove this for you:
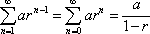
Where a is equal to first number in the series and r is equal to a common ratio (the number that is constantly being multiplied by in the sum of the series). For this series to be divergent, the common ratio must be greater than one. Now, why don't you give this example a try? Find the sum of the following series:
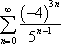
Geometric Series
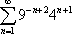
What is a Geometric Series?
A Geometric Series is a summation of a number. Usually, a Geometric Series is easily distinguishable by the number having it to the power of "n". If the summation formula is not given, it would be distinguishable by its constant product of the same number. Usually when deciding what type of test you should use on a test, read the instructions carefully. If it tells you to "find the sum of the following series", then you know that Geometric Series can possibly be used. This is how a Geometric Series would look like: