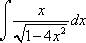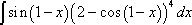Geometric
-
Integrals
Definite Integrals
Substitution
Integration by Parts
- References
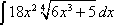
Now, this may seem a bit complicated, but let us do the first step. This step is to take the inner most function and make it equal to a variable. Let's call it "u"
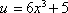
The next step is to take the derivative of u. We will call the derivative of u "du":
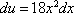
Now, look back at your equation. du is in the original equation! This is how you know you did the derivative correctly. Now, the next step is to replace all of your numbers with variables:
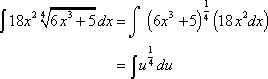
The final step is to take the integrand of your new equation. Remember to add a constant at the end. We put this because we do not know the exact constant being added and thus, we represent this constant as "C":
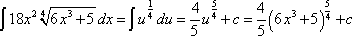
And there you have it! The final answer of this problem! Wasn't too bad right? Now I want you to do this problem yourself!
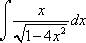
Substitution
What is Substituiton?
Substitution is a method of solving integrals. It involves taking an inner function and finding its derivative. In order for substitution to work, the derivative of the function must be present in the equation. However, there ara certain cases where the derivative is not in the equation. We will not be covering this on this site. For more information about this, see other Mathematic sites.
After finding the derivative, replace the original function by the variable you made it equate to. Once done, you take the integrand of the variable and replace your variable with the initial function that was set as your variable.
Now, let us look at some examples
Examples
Here is the first example (taken from Paul's Online Math Notes):
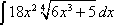
Now, this may seem a bit complicated, but let us do the first step. This step is to take the inner most function and make it equal to a variable. Let's call it "u"
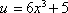
The next step is to take the derivative of u. We will call the derivative of u "du":
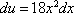
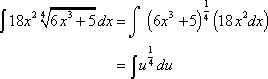
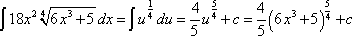
And there you have it! The final answer of this problem! Wasn't too bad right? Now I want you to do this problem yourself!